Simple Iteration over Variables with `lm()`
Note that this is not without shortcomings and lacks some flexibility, but it does keep you from having dig deep into how formulas actually work in R – which many (myself included) find confusing in the extreme.
For this example, let’s work with the standard mtcars dataset.
head(mtcars)## mpg cyl disp hp drat wt qsec vs am gear carb
## Mazda RX4 21.0 6 160 110 3.90 2.620 16.46 0 1 4 4
## Mazda RX4 Wag 21.0 6 160 110 3.90 2.875 17.02 0 1 4 4
## Datsun 710 22.8 4 108 93 3.85 2.320 18.61 1 1 4 1
## Hornet 4 Drive 21.4 6 258 110 3.08 3.215 19.44 1 0 3 1
## Hornet Sportabout 18.7 8 360 175 3.15 3.440 17.02 0 0 3 2
## Valiant 18.1 6 225 105 2.76 3.460 20.22 1 0 3 1The function, lm_caller()
The function we will make – lm_caller() – is rather dull at its core. It just takes in different arguments for the left-hand side (LHS), right-hand side (RHS) and data of an model you want to fit.
lm_caller <- function(LHS, RHS, data){
formula <- as.formula(paste0(LHS, " ~ ", RHS))
output <- lm(formula, data = data)
return(output)
}Run the function manually
model_1 <- lm_caller(LHS = "mpg", RHS = "disp + wt", data = mtcars)
summary(model_1)##
## Call:
## lm(formula = formula, data = data)
##
## Residuals:
## Min 1Q Median 3Q Max
## -3.4087 -2.3243 -0.7683 1.7721 6.3484
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 34.96055 2.16454 16.151 4.91e-16 ***
## disp -0.01773 0.00919 -1.929 0.06362 .
## wt -3.35082 1.16413 -2.878 0.00743 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 2.917 on 29 degrees of freedom
## Multiple R-squared: 0.7809, Adjusted R-squared: 0.7658
## F-statistic: 51.69 on 2 and 29 DF, p-value: 2.744e-10Iterate (apply) over many dependent and independent variables
First, make a big ol’ list of the different combinations of variables you want in your models:
left_hand_side <- data.frame(lhs = c('mpg', 'hp', 'am'))
right_hand_side <- data.frame(rhs = c('cyl', 'disp', 'wt', 'qsec', 'disp + wt', 'cyl - 1'))Now do a nested apply() over each of those
model_list <- apply(left_hand_side, 1, function(lhs){
apply(right_hand_side, 1,function(rhs){
lm_caller(LHS = lhs, RHS = rhs, data = mtcars)
})
})One major downside to munging strings for model specification is that the formula stored in the resulting models will all look identical:
model_list[[1]][1:2]## [[1]]
##
## Call:
## lm(formula = formula, data = data)
##
## Coefficients:
## (Intercept) cyl
## 37.885 -2.876
##
##
## [[2]]
##
## Call:
## lm(formula = formula, data = data)
##
## Coefficients:
## (Intercept) disp
## 29.59985 -0.04122Mapping these models back to their original data is a bit of a pain. There is a way to do it that I find much cleaner, so long as you are willing to. . .
Do it tidy!
If this approach make sense to you, I would recommend this basic tutorial on functional programming with purrr in R and this book chapter on building many models, utilizing the power of the tidyverse
First, make a data frame of all the left- and right-hand sides, so we can keep track of them:
formulae_dat <- tidyr::crossing(left_hand_side, right_hand_side)
head(formulae_dat)## # A tibble: 6 x 2
## lhs rhs
## <fct> <fct>
## 1 am cyl
## 2 am cyl - 1
## 3 am disp
## 4 am disp + wt
## 5 am qsec
## 6 am wtNow, add the models to this, with the help of mutate() and map2
Note we could also change up the dataset as part of this (not sure why you’d want to), but that would require using pmap() instead of map2
model_dat <- dplyr::mutate(formulae_dat,
model = purrr::map2(lhs, rhs, function(lhs, rhs){
lm_caller(LHS = lhs, RHS = rhs, data = mtcars)
})
)head(model_dat)## # A tibble: 6 x 3
## lhs rhs model
## <fct> <fct> <list>
## 1 am cyl <lm>
## 2 am cyl - 1 <lm>
## 3 am disp <lm>
## 4 am disp + wt <lm>
## 5 am qsec <lm>
## 6 am wt <lm>Having models inside of a dataframe might not seem any more helpful, but you can write a function to extract the parts that you really want. Or, rely on broom for more common models.
Note here I’m using lambda style function specification, rather than the more verbose function(x){} format.
model_dat <- dplyr::mutate(model_dat,
model_summary = purrr::map(model, ~broom::glance(.x)),
model_coefficient = purrr::map(model, ~broom::tidy(.x))
)
head(model_dat)## # A tibble: 6 x 5
## lhs rhs model model_summary model_coefficient
## <fct> <fct> <list> <list> <list>
## 1 am cyl <lm> <tibble [1 × 11]> <tibble [2 × 5]>
## 2 am cyl - 1 <lm> <tibble [1 × 11]> <tibble [1 × 5]>
## 3 am disp <lm> <tibble [1 × 11]> <tibble [2 × 5]>
## 4 am disp + wt <lm> <tibble [1 × 11]> <tibble [3 × 5]>
## 5 am qsec <lm> <tibble [1 × 11]> <tibble [2 × 5]>
## 6 am wt <lm> <tibble [1 × 11]> <tibble [2 × 5]>Now, with an unnest, we can access the most relevant parts of each model.
tidyr::unnest(model_dat[,c(-3,-5)], model_summary)## # A tibble: 18 x 13
## lhs rhs r.squared adj.r.squared sigma statistic p.value df logLik
## <fct> <fct> <dbl> <dbl> <dbl> <dbl> <dbl> <int> <dbl>
## 1 am cyl 0.273 0.249 0.432 11.3 2.15e- 3 2 -17.5
## 2 am cyl … 0.253 0.229 0.560 10.5 2.84e- 3 1 -26.3
## 3 am disp 0.350 0.328 0.409 16.1 3.66e- 4 2 -15.8
## 4 am disp… 0.482 0.446 0.371 13.5 7.17e- 5 3 -12.1
## 5 am qsec 0.0528 0.0213 0.494 1.67 2.06e- 1 2 -21.8
## 6 am wt 0.480 0.462 0.366 27.6 1.13e- 5 2 -12.2
## 7 hp cyl 0.693 0.683 38.6 67.7 3.48e- 9 2 -161.
## 8 hp cyl … 0.939 0.937 40.5 476. 2.23e-20 1 -163.
## 9 hp disp 0.626 0.613 42.6 50.1 7.14e- 8 2 -164.
## 10 hp disp… 0.635 0.609 42.9 25.2 4.57e- 7 3 -164.
## 11 hp qsec 0.502 0.485 49.2 30.2 5.77e- 6 2 -169.
## 12 hp wt 0.434 0.415 52.4 23.0 4.15e- 5 2 -171.
## 13 mpg cyl 0.726 0.717 3.21 79.6 6.11e-10 2 -81.7
## 14 mpg cyl … 0.734 0.725 11.0 85.5 2.02e-10 1 -122.
## 15 mpg disp 0.718 0.709 3.25 76.5 9.38e-10 2 -82.1
## 16 mpg disp… 0.781 0.766 2.92 51.7 2.74e-10 3 -78.1
## 17 mpg qsec 0.175 0.148 5.56 6.38 1.71e- 2 2 -99.3
## 18 mpg wt 0.753 0.745 3.05 91.4 1.29e-10 2 -80.0
## # … with 4 more variables: AIC <dbl>, BIC <dbl>, deviance <dbl>,
## # df.residual <int>tidyr::unnest(model_dat[,-3:-4], model_coefficient)## # A tibble: 36 x 7
## lhs rhs term estimate std.error statistic p.value
## <fct> <fct> <chr> <dbl> <dbl> <dbl> <dbl>
## 1 am cyl (Intercept) 1.31 0.280 4.68 0.0000571
## 2 am cyl cyl -0.146 0.0435 -3.36 0.00215
## 3 am cyl - 1 cyl 0.0498 0.0154 3.24 0.00284
## 4 am disp (Intercept) 0.955 0.155 6.18 0.000000855
## 5 am disp disp -0.00238 0.000593 -4.02 0.000366
## 6 am disp + wt (Intercept) 1.60 0.276 5.81 0.00000266
## 7 am disp + wt disp 0.000451 0.00117 0.386 0.703
## 8 am disp + wt wt -0.404 0.148 -2.73 0.0108
## 9 am qsec (Intercept) 1.55 0.890 1.74 0.0914
## 10 am qsec qsec -0.0642 0.0496 -1.29 0.206
## # … with 26 more rowsFunctions like filter() and ggplot() are extremely useful at this point to get a beter feel for what your mnodels are actually saying, but we will save that for another time.
Plot from multiple models with ggplot
library(tidyverse, quietly = T)## ── Attaching packages ───────────────────────────────────────────────────────────────────────────────── tidyverse 1.3.0 ──## ✓ ggplot2 3.3.0 ✓ purrr 0.3.3
## ✓ tibble 3.0.0 ✓ dplyr 1.0.0
## ✓ tidyr 1.0.2 ✓ stringr 1.4.0
## ✓ readr 1.3.1 ✓ forcats 0.5.0## ── Conflicts ──────────────────────────────────────────────────────────────────────────────────── tidyverse_conflicts() ──
## x dplyr::filter() masks stats::filter()
## x dplyr::lag() masks stats::lag()model_dat %>%
unnest(model_coefficient) %>%
mutate(
low = estimate - std.error,
high = estimate + std.error,
formula = paste(lhs, "~", rhs)
) %>%
ggplot(aes(estimate, term, xmin = low, xmax = high, height = 0)) +
geom_vline(xintercept = 0, color = 'grey50') +
geom_errorbarh() +
geom_point() +
geom_text(aes(label = round(p.value, 3)), nudge_y = 0.33, ) +
facet_wrap(vars(formula), scales = 'free', ncol = 2) 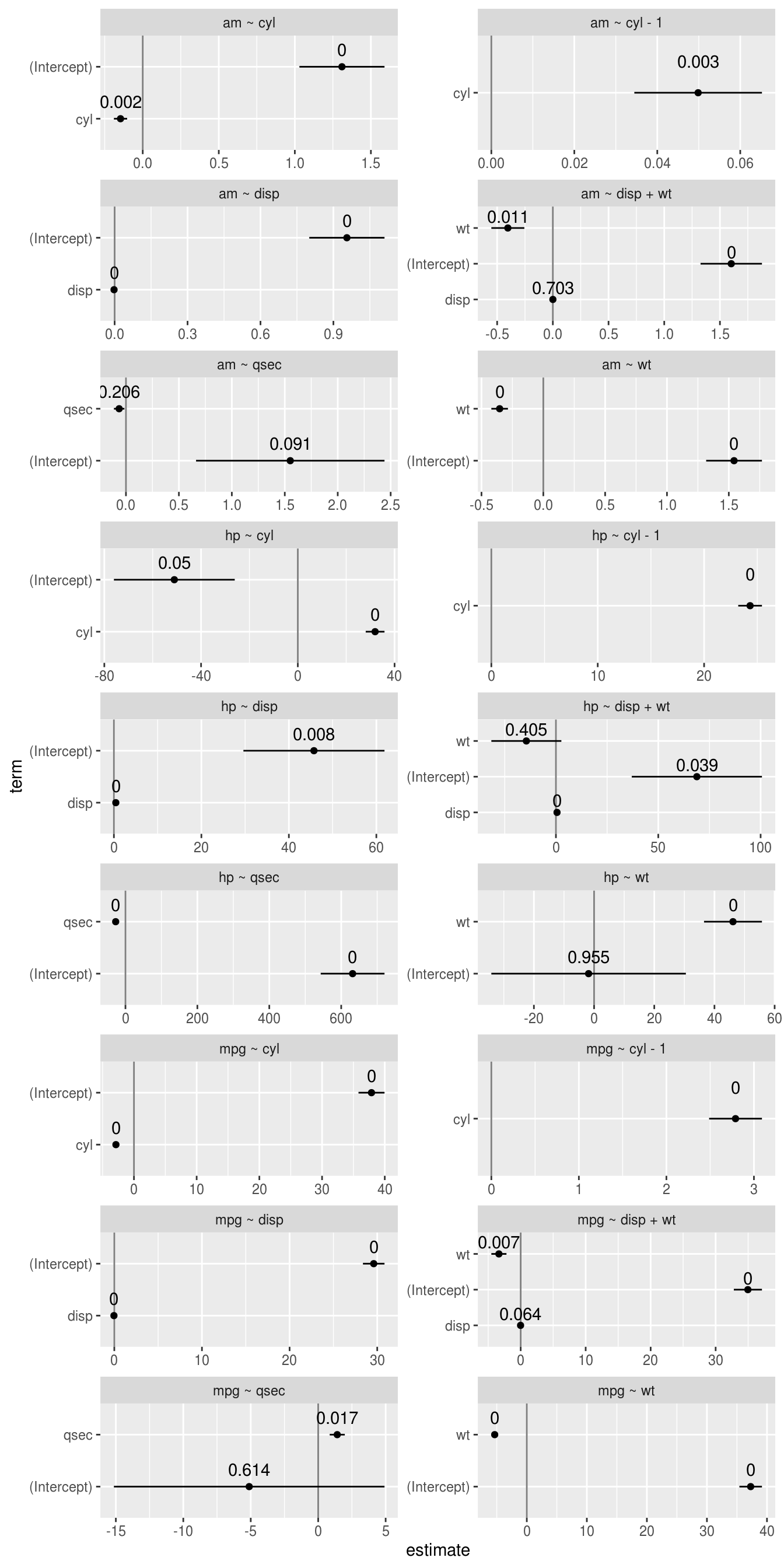
model_dat %>%
unnest(model_coefficient) %>%
filter(str_detect(rhs, "cyl")) %>%
mutate(
low = estimate - std.error,
high = estimate + std.error
) %>%
ggplot(aes(estimate, term, xmin = low, xmax = high, height = 0)) +
geom_vline(xintercept = 0, color = 'grey50') +
geom_errorbarh() +
geom_point() +
geom_text(aes(label = round(p.value, 3)), nudge_y = 0.33, ) +
facet_grid(rows = vars(lhs), cols = vars(rhs), scales = 'free') 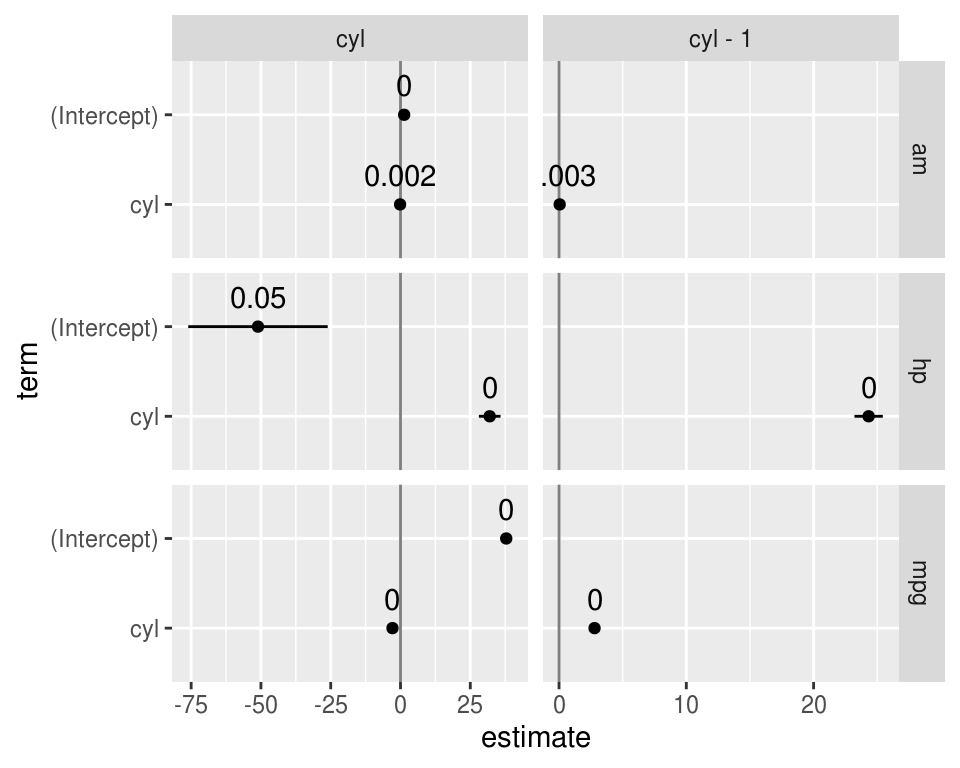
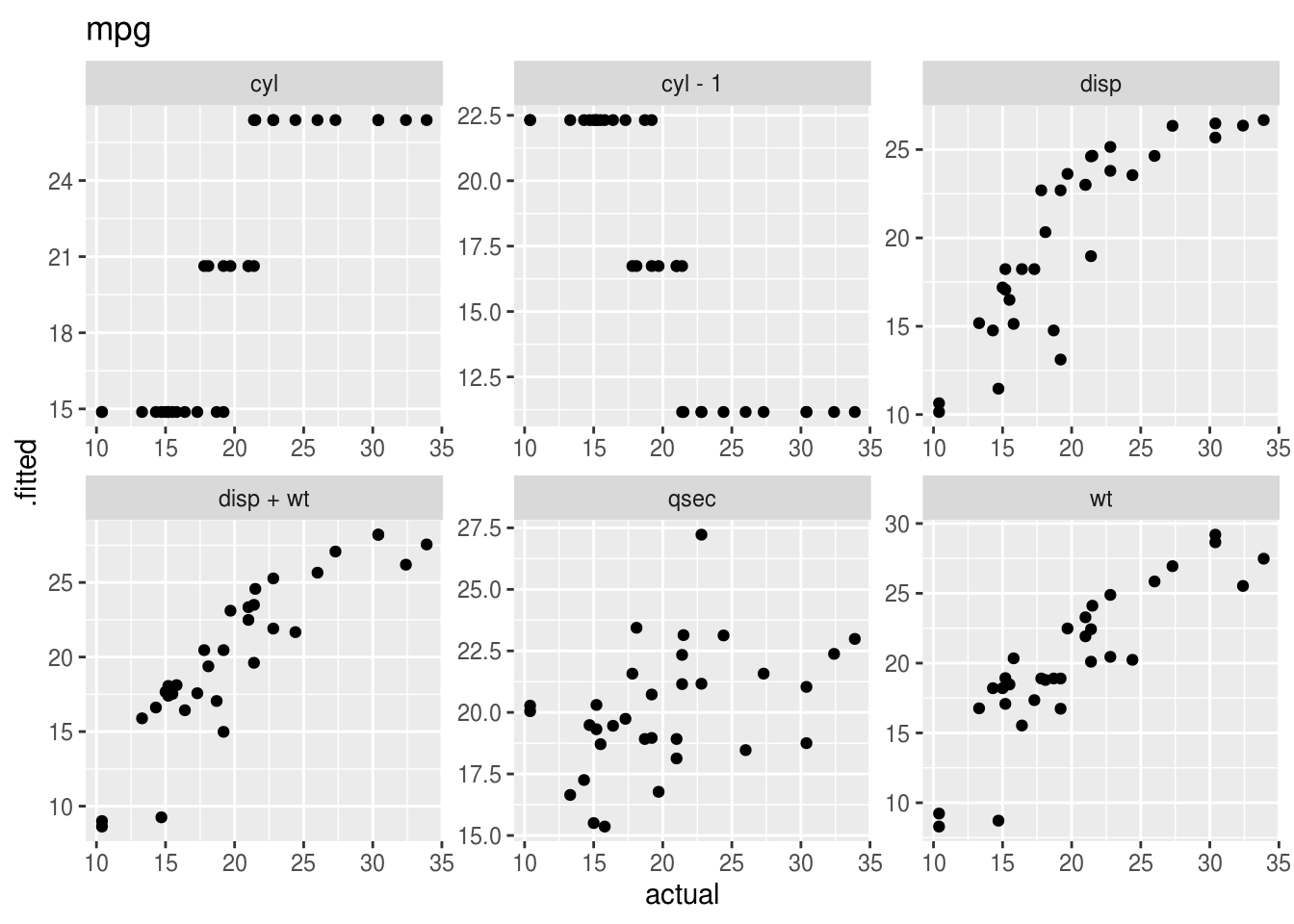
Plotting the “acutal” vs “predicted” (fitted) values takes a bit of work with pivot_longer(), and is probably best done separately for each outcome variable.
Remember that ggplots are actually objects, so we can actually stick them into a dataframe and then plot them later!
plot_dat <- model_dat %>%
mutate(model_resid = map(model, broom::augment)) %>%
select(lhs, rhs, model_resid) %>%
unnest(model_resid) %>%
pivot_longer(cols = c(-starts_with("."), -lhs, -rhs),
names_to = 'name',
values_to ='actual'
) %>%
filter(lhs == name) %>%
nest(data = -lhs) %>%
mutate(plot = map2(data, lhs, ~(
ggplot(.x, aes(x = actual, y = .fitted, height = 0)) +
geom_point() +
facet_wrap(~rhs, scales = 'free') +
labs(title = .y)
)))
plot_dat## # A tibble: 3 x 3
## lhs data plot
## <fct> <list> <list>
## 1 am <tibble [192 × 11]> <gg>
## 2 hp <tibble [192 × 11]> <gg>
## 3 mpg <tibble [192 × 11]> <gg>plot_dat$plot## [[1]]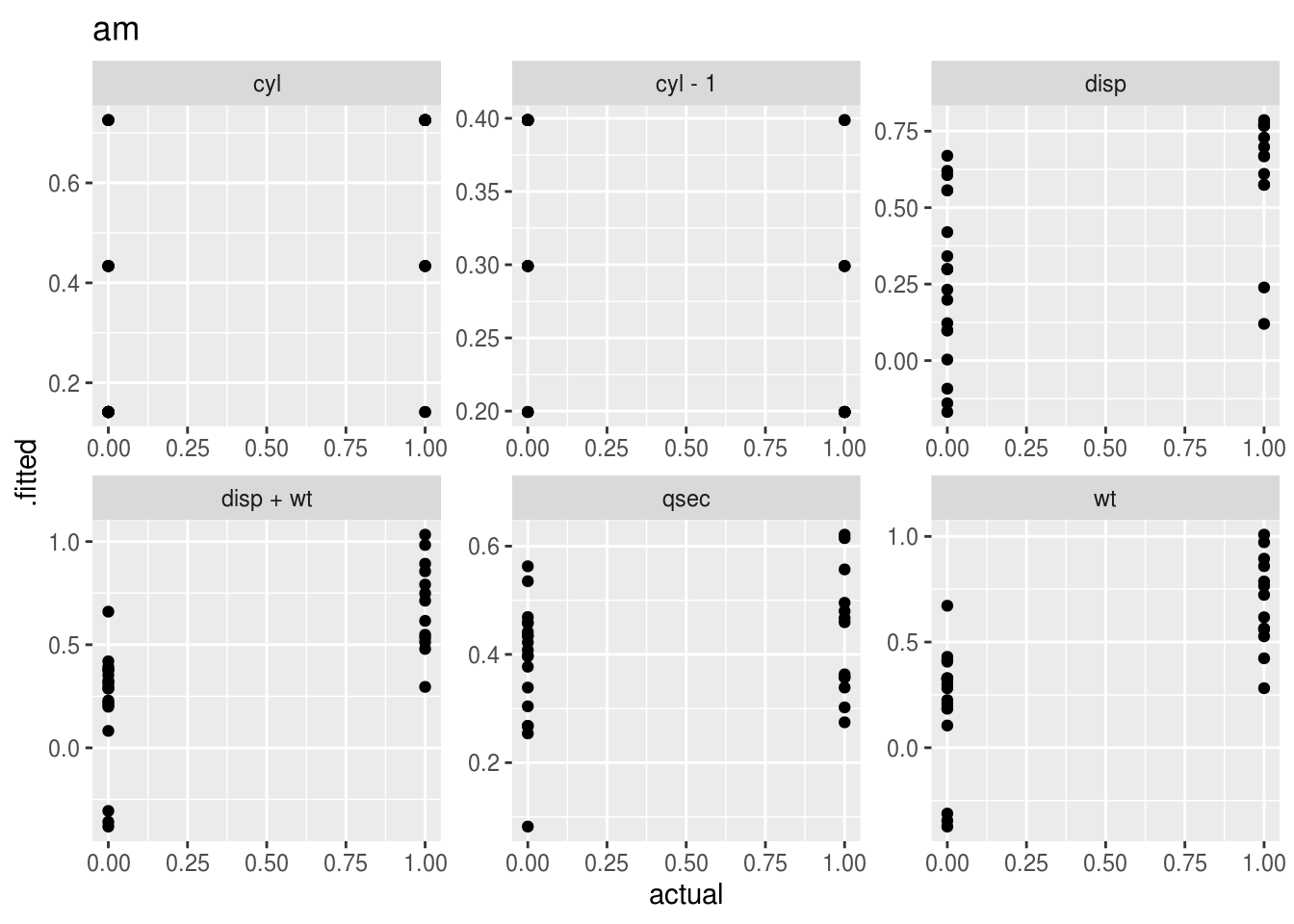
##
## [[2]]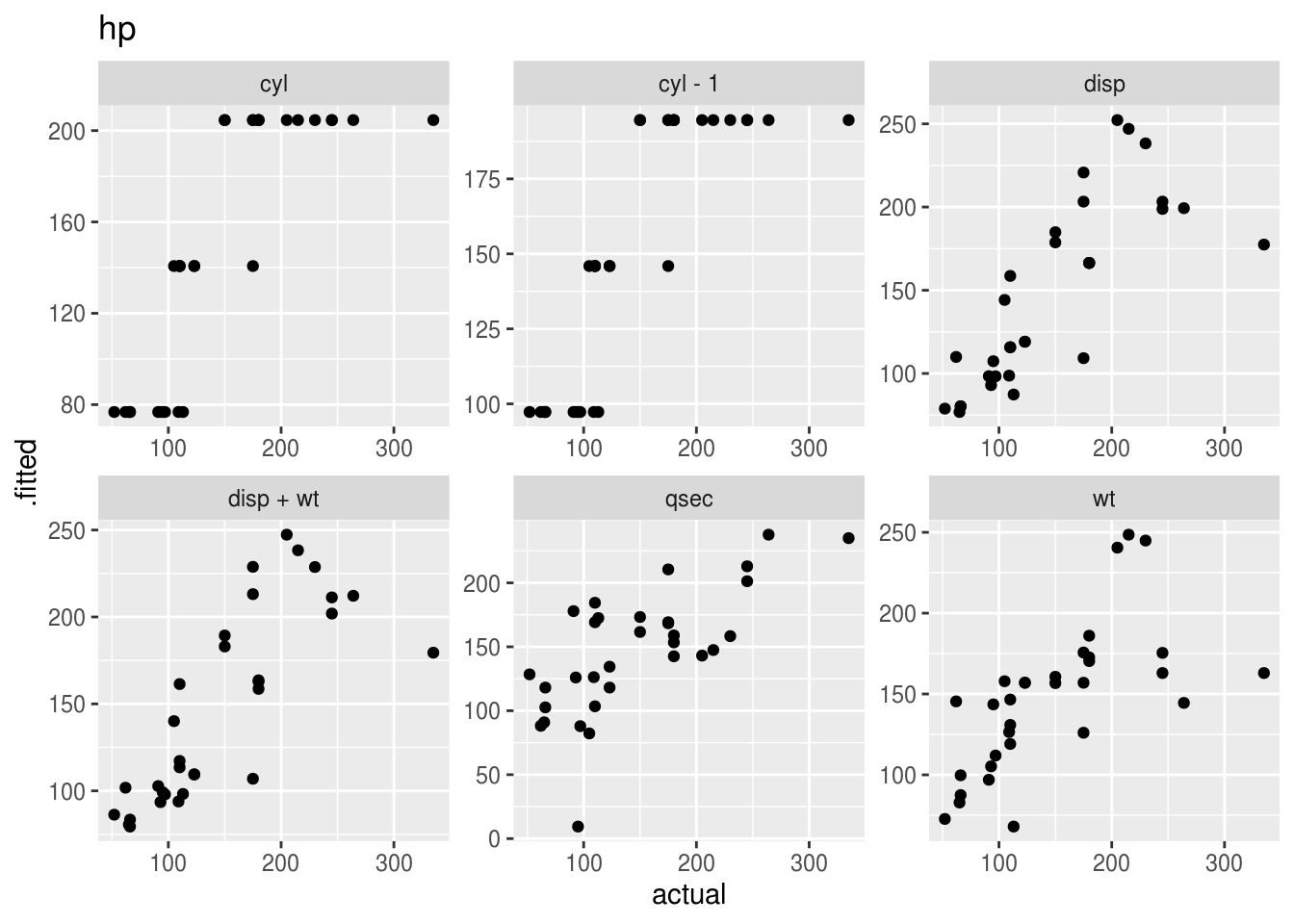
##
## [[3]]